natural experiments
natural experiments
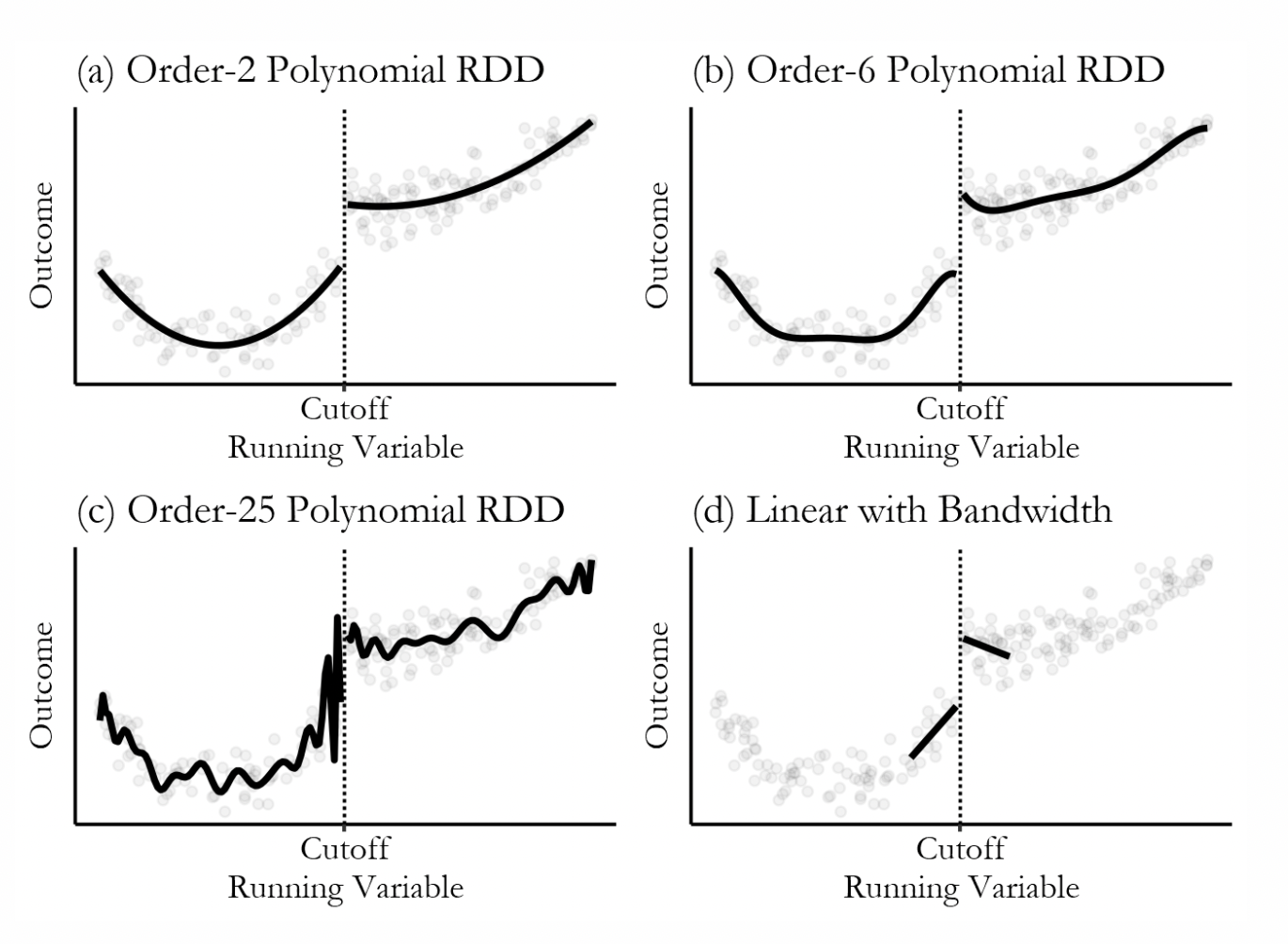
regression discontinuity design
doordash case study
inspired by jessica lachs and matheus facure alves
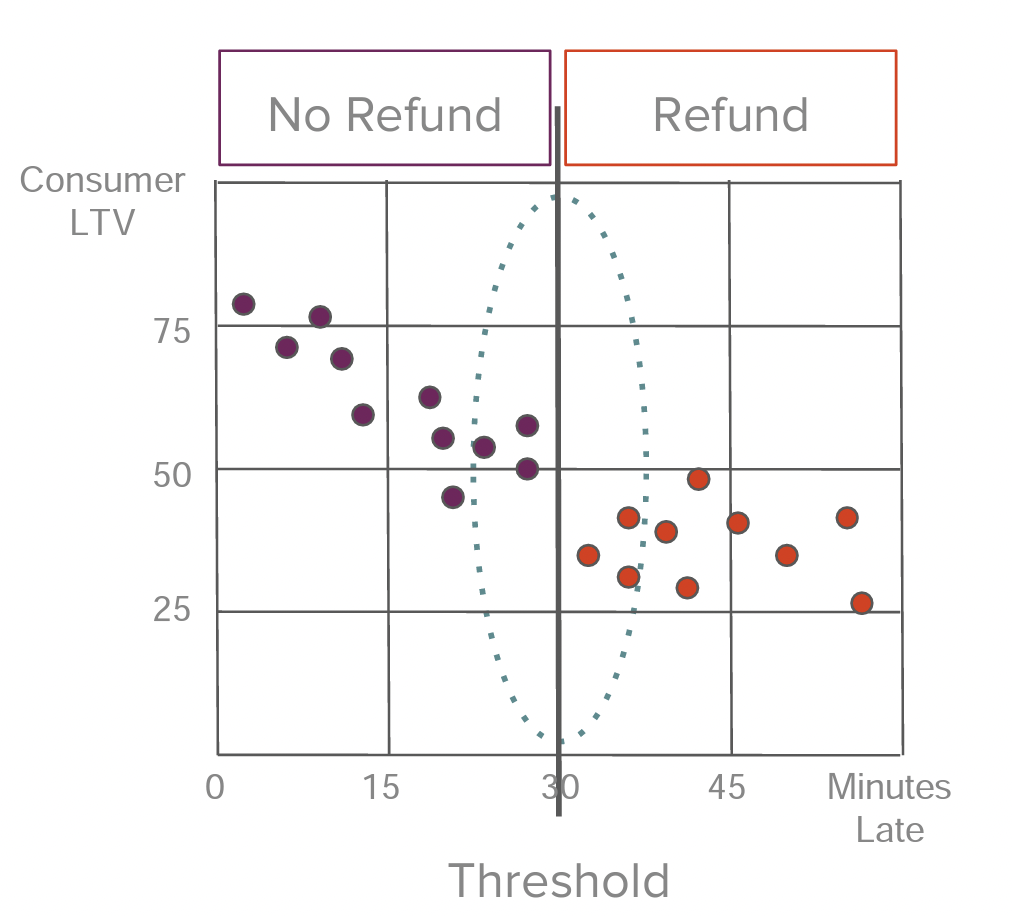
"hangry" customers 👉 lost customers?
do refunds save customer ltv to some degree?
- a/b testing: unfair to randomly assign refunds
- refund vs. no refund: average lateness differs
confounding!
refund
ltv
min late
"hangry" customers 👉 lost customers?
do refunds save customer ltv to some degree?
- continuity: relationship between ltv and lateness is naturally smooth
- "as good as random": treatment is randomly assigned to near winners and near losers
order lateness determines treatment 👉 cutoff: 30 minutes
- "near-loser": 29.9 min late
- "near-winner": 30.1 min late
look for a jump!
"hangry" customers 👉 lost customers?
do refunds save customer ltv to some degree?
Y_i = \beta_0 + \beta_1(R_i - c) + \beta_2\mathbb{1}_{R_i \geq c} + \beta_3 (R_i - c)\cdot \mathbb{1}_{R_i \geq c} + \epsilon
running variable: min late
cutoff: 30 min
treatment: 1 - yes; 0 - no
"as good as random"
treated:
(\beta_0 + \beta_2) + (\beta_1 + \beta_3)\cdot(R_i - c) + \epsilon
\beta_0
intercept at cutoff
intercept at cutoff
\beta_2 + \beta_0
treatment effect:
(\beta_0 + \beta_2) - \beta_0 = \beta_2
untreated:
\beta_0 + \beta_1(R_i - c) + \epsilon
interaction: min late may affect ltv differently on each side
def generate_dataset(n, std, b0, b1, b2, b3, lower=0, upper=60, cutoff=30):
"""generate customer LTV under given order lateness and refund status"""
# generate running variable, treatment status, and errors
min_late = np.random.uniform(lower, upper, n)
was_refunded = np.where(min_late < cutoff, 0, 1)
errors = np.random.normal(0, std, n)
# use above data to "predict" customer LTV
ltv = (
b0
+ b1 * (min_late - cutoff)
+ b2 * was_refunded
+ b3 * (min_late - cutoff) * was_refunded
+ errors
)
# return results in a dataframe
df_late = pd.DataFrame({"min_late": min_late, "ltv": ltv})
df_late["min_late_centered"] = df_late["min_late"] - cutoff
df_late["refunded"] = df_late["min_late"].apply(lambda x: 1 if x >= cutoff else 0)
return df_late
# generate data on 2,000 late orders
df_late = generate_dataset(n=2000, std=10, b0=50, b1=-0.8, b2=10, b3=-0.1)# DATA PREPARATION
generate toy data
# generate data for 2,000 late orders
df_late = generate_dataset(2000, 10)
df_late.head()# DATA PREPARATION
generate toy data
modeling
data viz
import statsmodels.formula.api as smf
# fit model
model_all_data = smf.wls("ltv ~ min_late_centered * refunded", df_late).fit()
# model summary
model_all_data.summary().tables[1]# USING ALL DATA
regress on all data
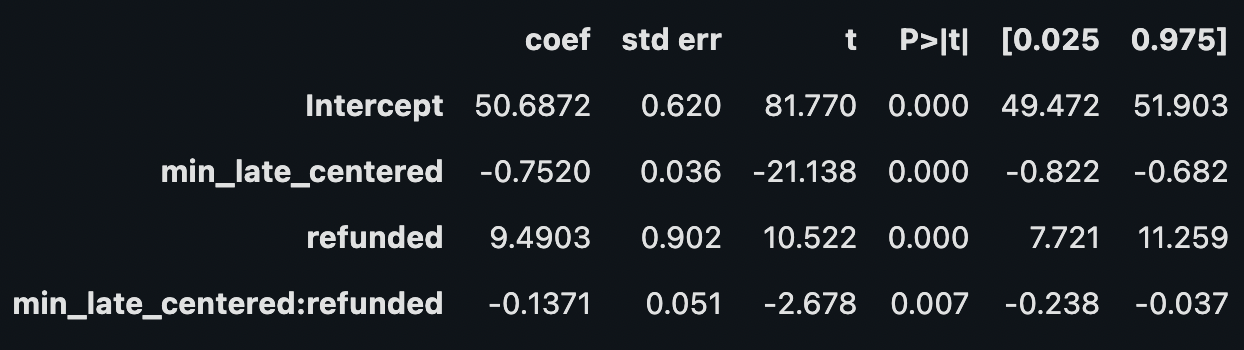
treatment effect: 9.49
# USING ALL DATA
regress on all data
treatment effect: 9.49
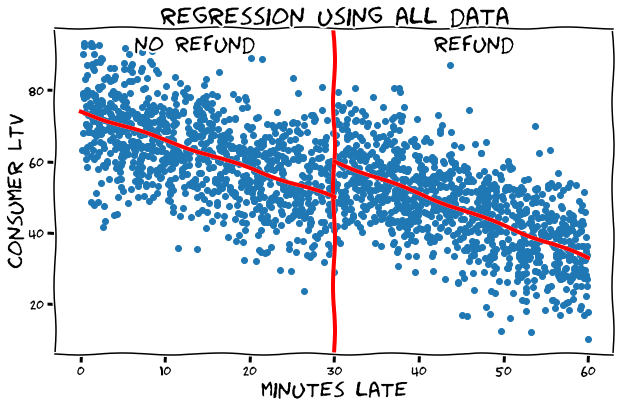
what about just comparing near-losers vs. near-winners?
def kernel(min_late, cutoff, bandwidth):
"""assign weight to each data point (0 if outside bandwdith)"""
# assign weight based on distance to cutoff
weight = np.where(
np.abs(min_late - cutoff) <= bandwidth,
(1 - np.abs(min_late - cutoff) / bandwidth),
0.0000000001, # ≈ 0 outside bandwidth (not 0 to avoid division by 0)
)
# return weight of each data point
return weight
df_late["weight"] = df_late["min_late"].apply(lambda x: kernel(x, 30, 5))# KERNEL WEIGHTING
assign kernel weights to data
- outside bandwidth: not considered
- within bandwidth: closer to cutoff 👉 higher weight
\mathbb{1}_{|R_i - c|\geq h} \cdot (1 - \frac{|R_i - c|}{h})
indicates whether point is within bandwidth
# KERNEL WEIGHTING
assign kernel weights to data
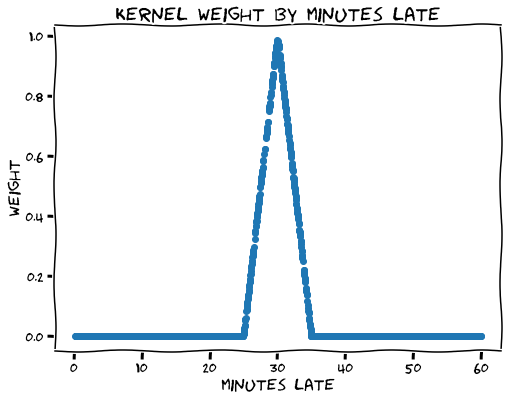
# KERNEL WEIGHTING
regress near cutoff
# fit model using weighted data
model_kernel_weight = smf.wls(
"ltv ~ min_late_centered * refunded",
df_late,
weights=df_late["weight"],
).fit()
# model summary
model_kernel_weight.summary().tables[1]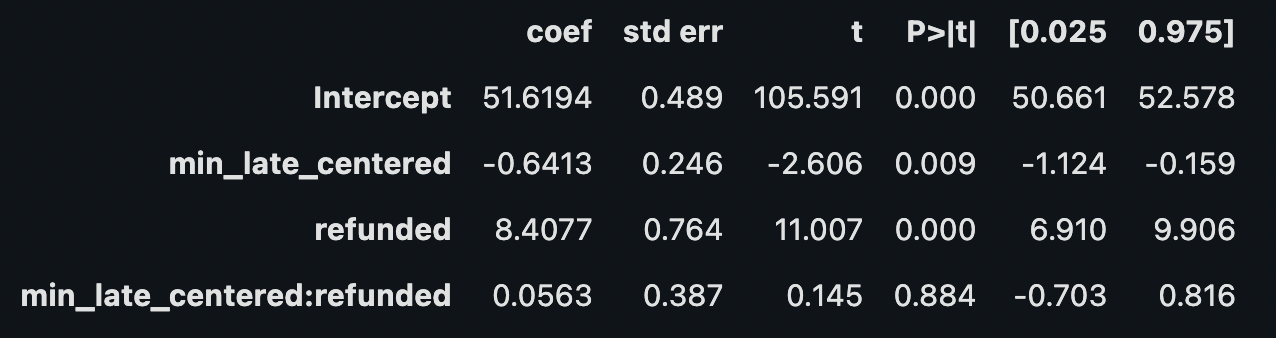
treatment effect: 8.41
# KERNEL WEIGHTING
regress near cutoff
treatment effect: 8.41
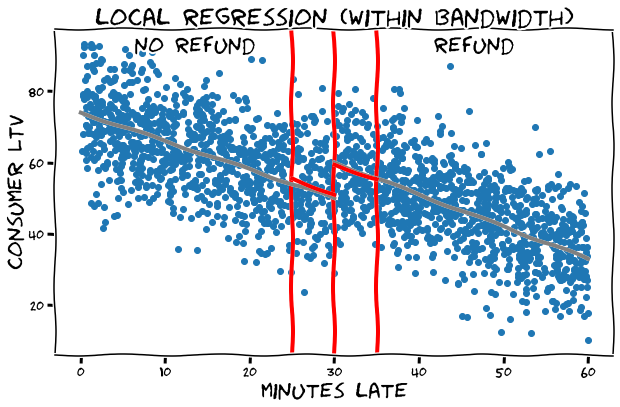
complications of rdd
- optimal bandwidth: use expertise or data-driven methods (cross-validation, imbens & kalyanaraman, 2012)
- not as good as random: e.g., rule-makers manipulate cutoff to include/exclude certain individuals, individuals try to get "mercy pass"
-
fuzziness: "cutoff" impacts the treatment probability but offers no guarantee
- problem: underestimate treatment effect 👉 those below threshold may get treatment and those above may not
- solution: instrumental variables 👉 estimate effect based on actually treated vs. untreated units
- non-linearity: use polynomial regression or local regression (e.g., loess, lowess)
# OTHER NATURAL EXPERIMENTS
veil-of-darkness test
- natural experiment: when daylight saving begins, it gets darker later 👉 7 pm might be dark yesterday but still light today
- outcome: % of black drivers stopped by police at 7 pm increase today? 👉 if so, race may causally impact police stop decisions
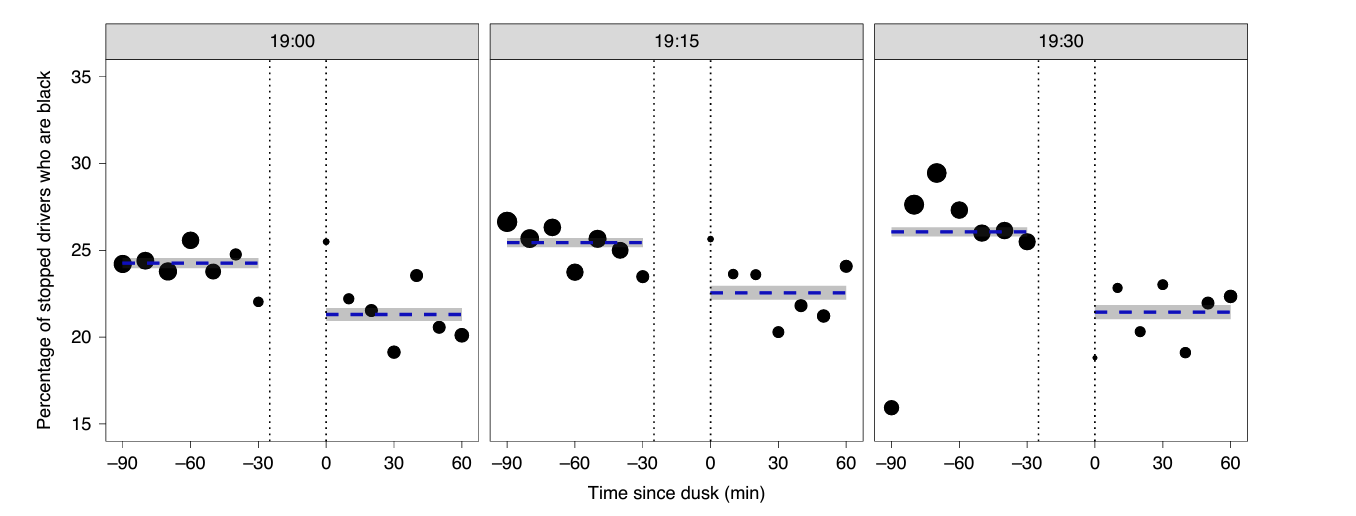
stanford open policing project (pierson et al., 2020)
# OTHER NATURAL EXPERIMENTS
instrumental variables
birth season
schooling
income
confounders
\kappa = \frac{\mathrm{reduced}\, \mathrm{form}}{1\mathrm{st}\, \mathrm{stage}} = \frac{\mathrm{IV}\, \mathrm{on} \, \mathrm{outcome}}{\mathrm{IV}\, \mathrm{on} \, \mathrm{treatment}}
which we can easily find, but don't care about
scale to estimate how treatment affects outcome
1. causally impacts treatment
2. correlated with outcome
3. unrelated to confounders
summary
- why know why: so we can make things happen
- gold standard: randomized controlled trials (a/b testing)
- natural experiments: as good as random, but hard to come by
- statistical control: close "back-door paths"
- counterfactuals: fancier case studies
income
education
intelligence
grades
further resources
books + papers + talks
further resources
an example syllabus...